Clustering MNIST digits with Self-organizing Maps
I read about self-organizing maps being used to solve the traveling salesman problem in a blog post and was intrigued by it. I was surprised that self-organizing maps could be used to get good, though not optimal, solutions to such a difficult problem.
When I read more about it, its basic algorithm didn’t seem too difficult. So I decided to have a go at it myself by seeing whether I can code it from scratch in PyTorch.
Git Repo here.
About Self-Organizing Maps
Self-organizing maps are sometimes known as Kohonen maps, after its inventor. The basic idea is to find a good way to map data samples to an array of neurons such that similar data samples “light up” neurons in the same vicinity of each other. Note that the use of the term “neuron” mostly has to do with the neuroscience context of its invention.
To go into slightly more detail, let me explain what I mean when I say that data samples light up the neurons. Consider you have an $(M \times N)$ array of neurons, a $(D\times M \times N)$ weight matrix called $W$and a $D$-dimensional data sample called $x$. One can think of $W$ as storing a $D$-dimensional model vector, $m$, in each of the neurons in the $(M \times N)$ neuron array, such that $m_{ij}$ is the model vector for the neuron on the $i$th row and $j$th column of the array.
The learning algorithm is very much like what you would see in metaheuristic optimization. You start by finding a winner neuron. This is the neuron, $n^*$, where $m_{ij}$ is closest to the sample $x$. In other words, $n^*$ is the neuron that lights up when the sample $x$ is presented to the self-organizing map.
$$ n^* = \underset{i,j}{\operatorname{argmin}}||x-m_{ij}||_2 $$
Then what you do is that you adjust all the $m$ vectors in the vicinity of $n^*$ towards $x$. To do this, we can define a neighbourhood Gaussian scaling factor between neurons $n^*$and $n_{ij}$ shown below,
$$ \eta(n^*, n_{ij}, R) = \exp \left(-\frac{||x-m_{ij}||_2}{2R^2}\right) $$
where $R$ is the radius within which the surrounding neurons are considered neighbours.
We update $m_{ij}$ according to the following rule.
$$ m_{ij}^{t+1} = m_{ij}^t + \alpha^t \eta(n^*, n_{ij}, R^t)(x - m_{ij}) $$
where $0\leq\alpha\leq 1$ is the learning rate and $m_{ij}^t$ is the model vector of the $(i, j)$-th neuron at the $t$-th iteration of the algorithm.
First thing to notice about the update rule is that it seeks to make $m_{ij}$ equal to $x$. Thus for $n^*$, $m^*$ will be very close to $x$ and $n^*$ will be more likely to light up the next time a sample similar to $x$ is presented to the self-organizing map. On top of that, we don’t just do this adjustment for $m^*$ but for all other surrounding neurons as well. This is such that similar samples will have the tendency to light up neurons in the same area of the neuron map.
Next, the purpose of $\eta$ is such that neurons far away from $n^*$ will hardly be affected at all but those close to $n^*$ will be adjusted significantly.
Lastly, note that $\alpha$ and $R$ are dependent on the iteration. Specifically, both of them decay with time. This is such that the adjustments and the size of the neighbourhood get smaller over time.
In this way, as we present more and more data samples to the neuron map, the update rule will ensure that similar samples light up neurons that are close to each other and vice versa, thus having a clustering effect as we shall see later.
Clustering MNIST digits
Experimental details
I applied the self-organizing map algorithm to MNIST digits on a $(50\times50)$ square neuron map with $\alpha=0.5$ and $R=50$. At each iteration, $\alpha$ and $R$ decay at a rate of 0.95.
The MNIST training data set was used to update $W$ and the test dataset was used to visualize the final results.
For those who are unfamiliar with the MNIST digits dataset, it is a dataset consisting of images of handwritten digits (0 to 9) such as the one below.
For more details, see the Git repo here.
Results
The training of $W$was halted after 90 epochs of showing the self-organizing map the training data set when $R$ was reduced to less than 0.5.
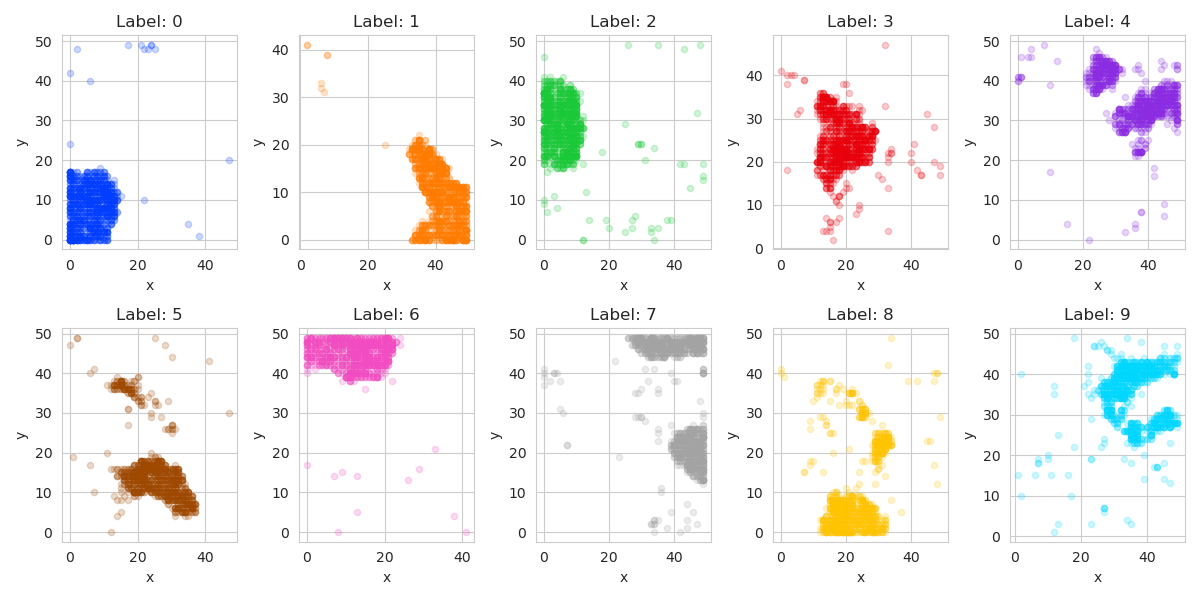
The figure below shows the neurons that light up for each MNIST digit. We can see that samples from each digit is mapped into a tight cluster in the neuron array (with some exceptions). This shows that the competitive learning algorithm manages to cluster the samples quite efficiently.
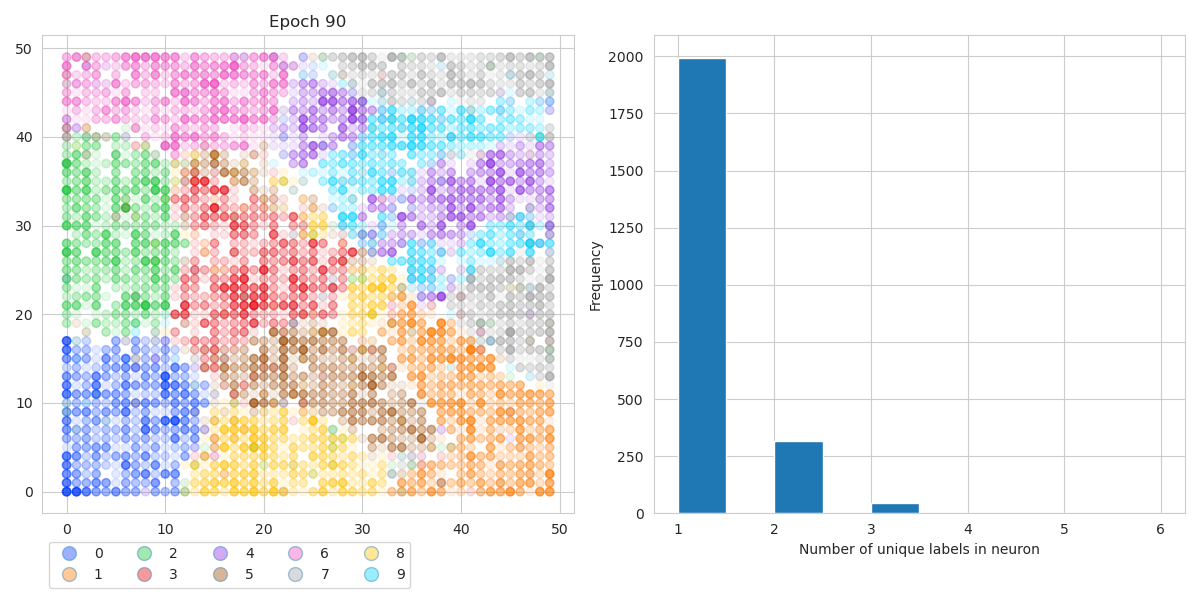
If we put all the activation maps together (see figure below, left panel) we can see that they are quite well segregated. On top of that, if we look at the right panel which shows the histogram of the number of unique digits that light up each neuron, we see that almost 2000 out of the 2500 neurons are only activated by 1 digit. This means that 80% of the neurons recognize a single digit very well.
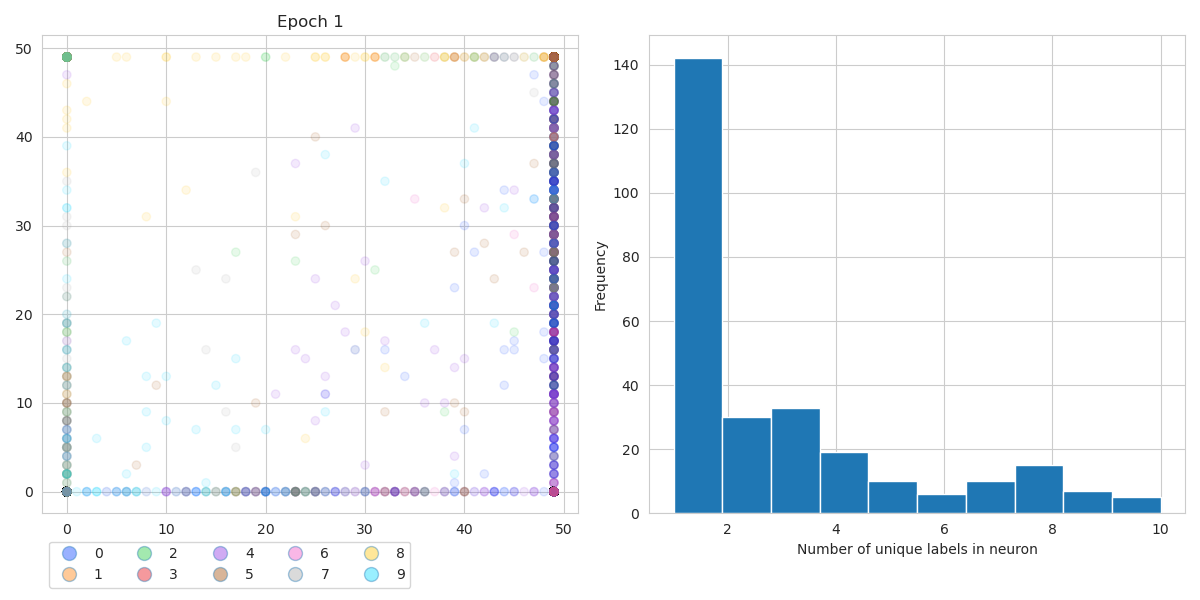
We can compare the same at the start of the training. See the figure below which shows the equivalent plots at Epoch 1 of the training process. We can see that only a few neurons are activated with lots of empty space in between activated neurons. And also, we see that there are many neurons that are activated by several digits. Some neurons are even activated by all 10 of the MNIST digits!
Other thoughts
Higher dimensions or other neuron array topologies
In this experiment, I used a 2D square array of neurons. But there is nothing stopping us from using other neuron arrangements. One can use a ring, like that used to solve the traveling salesman problem or a hexagonal grid. Maybe even a N-dimensional block!
Results are not unique
It must be noted that the final neuron activation maps are not unique. There is no guarantee that you will always end up with the same $W$ . It depends on how $W$ is initialised as well as the order in which the samples are presented to the self-organizing map.
Final thoughts
I was pleasantly surprised at how effective the self-organizing map was given that it was such a breeze to code. PyTorch allowed me to use my GPU for training. More importantly, I can see many uses for self-organizing maps where the maps are then used as inputs to other learning algorithms. For example, in this case, I could pass the activation maps to a classifier that would perform the classification of the MNIST digits.